Let’s address the first matter of business right away: What does cannibalism mean in cosmology? Just like how an animal is cannibalistic if it devours an animal of the same species, we can also have a fundamental particle that devours itself. To give some context, consider a plasma of particles that is slowly cooling due to the expansion of the universe. When the temperature of the plasma falls below the mass of one of the particles in it, the laws of thermodynamics force that particle to annihilate into lighter particles. However, if there are no other lighter particles, then that particle could annihilate into itself! For instance three of those particles could come together, annihilate, and then produce two highly energetic particles of the same species. Hence, such a particle is also fondly called a cannibal.
Unfortunately, of the known particles in the Standard Model, there aren’t any cannibals. This is because the lightest particle in the Standard Model is photon, which is massless. So in the very early universe, when there was a plasma formed by Standard Model particles, all the particles had something lighter to annihilate into. However, if there existed a hidden sector of particles which formed a plasma of their own, and if the lightest particle in that sector had a non-zero mass, then that lightest particle could naturally be a cannibal. The existence of a hidden sector is not that far-fetched of an idea, especially since the observed dark matter could naturally be a particle from such a hidden sector.
In this project we show that cannibalism in a hidden sector can leave imprint in the dark matter density distribution observed today. In particular, the energy density of the cannibal particle can determine the expansion rate of the universe in the first few seconds after the birth of the universe. The period where cannibal particle determines the expansion rate is called a “cannibal dominated era”. A cannibal dominated era causes the density fluctuations of dark matter to be more pronounced, with the peak enhancement determined by the strength of the cannibal annihilation reaction.
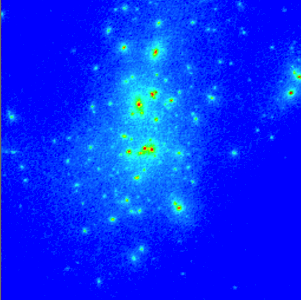
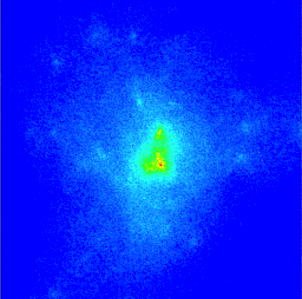
Such enhancement in the dark matter density fluctuations in the very early universe is known to produce microhalos of dark matter today. Adrienne Erickcek has worked extensively on the formation of such microhalos. Below is an image of a dark matter halo with (left) and without (right) an enhancement in dark matter density fluctuations (Note, the image is not part of our work).
As one can see, in the case where dark matter density fluctuations were enhanced in the early universe, the density distribution of dark matter is “clumpy” instead of smooth. The clumps are dark matter microhalos which come together to form a bigger halo. A clumpy dark matter distribution has the possibility to be detected in future observations.
Understanding radiation perturbations
This calculation was one of my favourite but unfortunately it couldn’t make it into the final paper. Basically I was able to analytically explain the rather odd evolution of radiation perturbation. This odd evolution of radiation perturbation had been encountered before in other scenarios as well, but its explanation had remained incomplete.
So what is this odd evolution I am talking about? Best to show this in a figure:
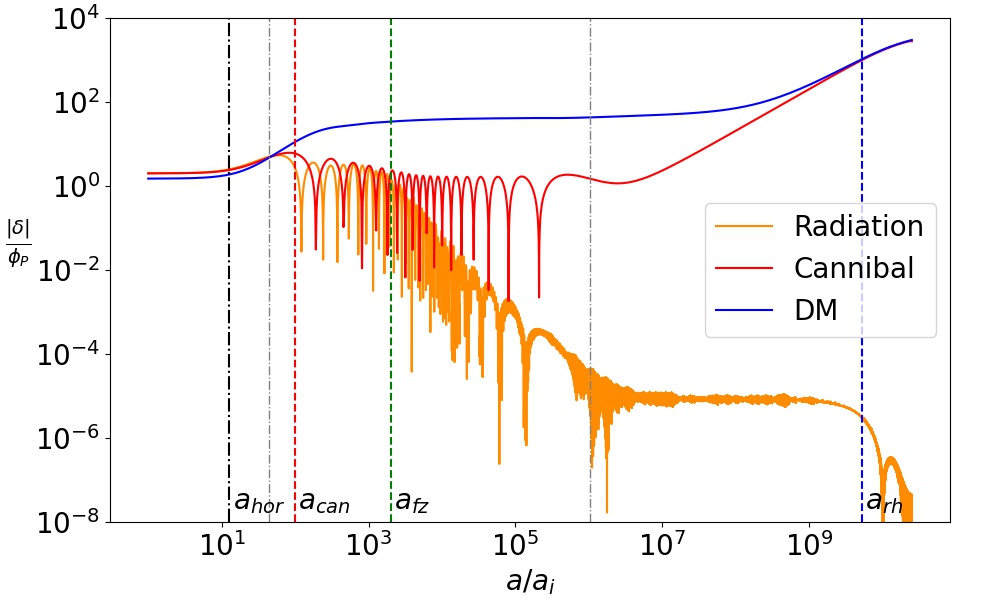
Above I show the evolution of the Fourier mode of the density perturbations in radiation, cannibal, and dark matter (DM). The evolution of cannibal and dark matter perturbations were somewhat straightforward to explain by looking at the equations which governed their evolution. However, the radiation perturbations were an enigma. It was not appparant why they were getting damped after ‘afz’ and after ‘arh’, or why they became constant for a while before ‘arh’.
Answering these question rigorously would require an analytical solution for the seven coupled differential equations that described this system. Luckily, it turned out that for the parameter space of our interest, several approximations could be made to simplify the differential equations. In particular, the equation for radiation perturbations simplified to a “forced damped harmonic oscillator equation”. Luckily, I had encountered this equation before when I was studying RLC circuits in my third year of engineering. It amazes me how mathematics is able to relate the description of voltage in RLC circuits to the evolution of perturbations in the first few seconds of the universe!
After a quick browse through my old engineering notes, I was able to apply the tools used to solve RLC circuits to solve radiation perturbation equations. In the figure below I show my analytical solutions as dot-dashed lines, which together are able to explain the evolution of radiation perturbation.
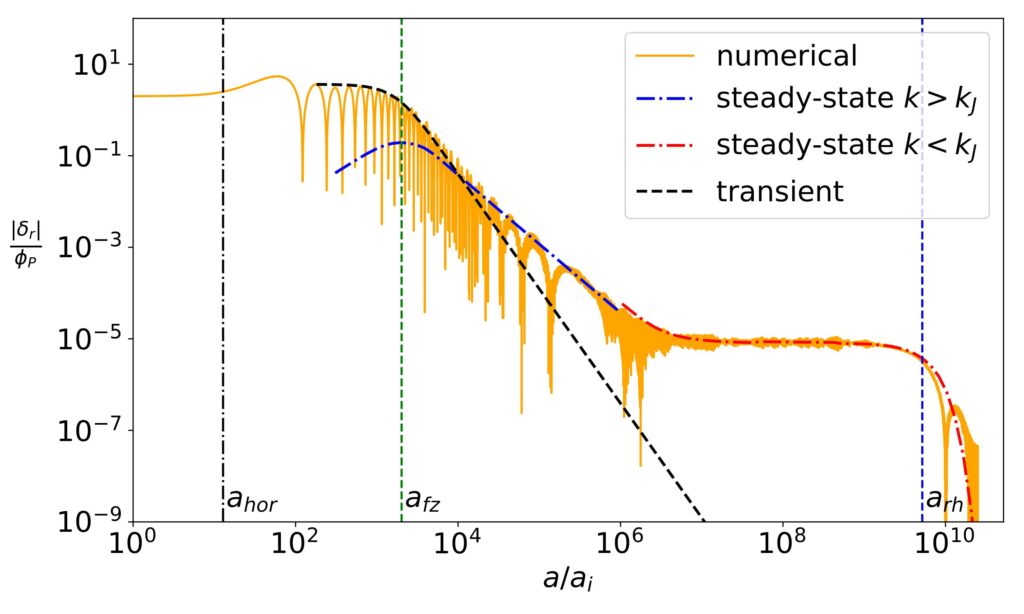
Unfortunately, all this effort was superfluos because, as we later learned, the radiation perturbations have almost no impact on dark matter perturbations. As the enhancement in the dark matter perturbations is the only potential observable for such early universe models, it is quite likely that the months of work I spent on understanding the behaviour of radiation perturbation would not be useful even in any other projects :'(