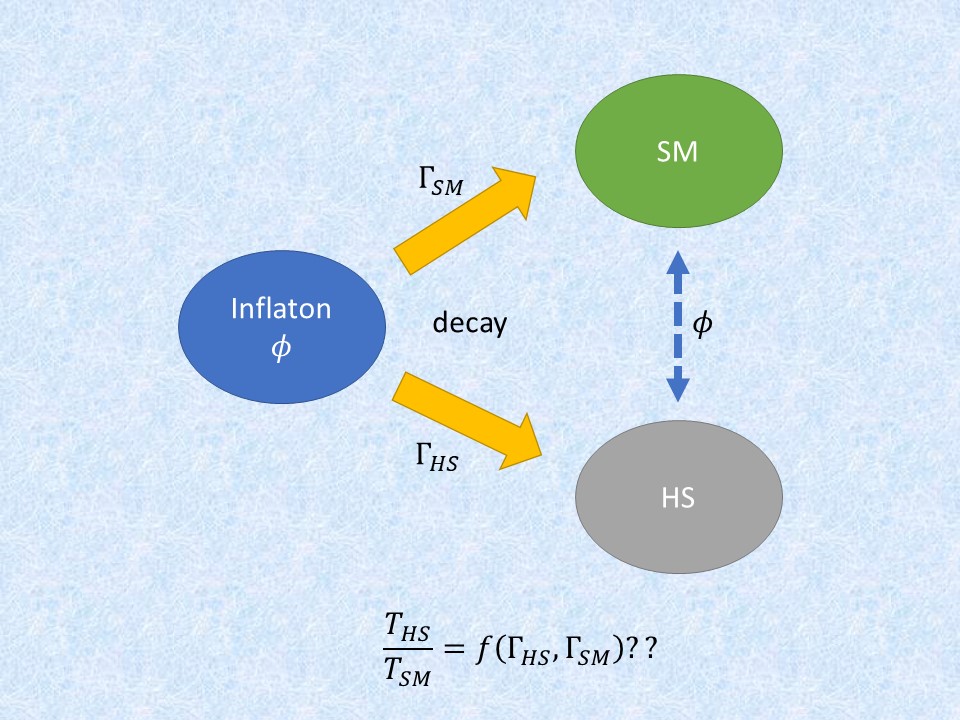
For a host of reasons (like explaining the temperature fluctuations in the cosmic microwave background, homogeneity and flatness of universe, etc.) we believe that the universe underwent a period of suuuperrr rapid expansion, called inflation, right after the universe was born. However this period of inflation must end and eventually produce the Standard Model particles (electrons, protons, photons, etc.) we know and love. The simplest way this transition can occur is if the field that causes inflation, called inflaton, decays into Standard Model particles. However, we also know that there is this additional unknown matter (dark matter) out there in the universe which is about 5 times more abundant than Standard Model particles and which seems to avoid any relationship with the Standard Model forces: Strong and Electroweak forces. One can then imagine a natural scenario where this dark matter is part of some hidden sector of particles who might have their own dark forces distinct from the Standard Model forces. If such a hidden sector exists, then the inflaton field should perhaps not choose favourites and have decay channels into both Standard Model particles and hidden sector particles.
The main goal of this project was to determine how the densities of the two sectors that are populated by inflaton decays depend on the inflaton decay rates into the two sectos. This relation between density and the decay rates is made non-trivial by the fact that the two sectors can interact with each other due to inflaton mediated interactions. Surprisingly, we found a simple relation for this seemingly complex system. When the reheat temperature (the temperature at which inflaton decays) is smaller than the inflaton mass, we find that the density ratio between the two sectors is proportional to the ratio of the inflaton decay rates. In contrast when the reheat temperature is larger than the inflaton mass, the density ratio is found to just depend on the smaller of the inflaton decay rate.
Above I tried to communicate (incompletely) the technical motivation and the outcome of this project. However, my main motivation when I accepted this project had little to do with the above motivation. This project was my first project as PhD student and also the first research project where I was the primary author. As a young grad student I could not concretely grasp the technical motivations I mentioned above. It was the buzz words: “inflation”, “hidden sector”, “dark forces”, etc., that made me more than excited to work on the project.
Quantum statistics hooplah in energy transfer rates
As it happens more often than not, I found the calculations involved in the project to be much more interesting than the results we finally got. One such calculation was evaluating the energy transfer rate due to inflaton mediated interactions from one sector to the other. The evaluation of this quantity is hard because it involves performing integration over 8 dimensional phase space. However, by assuming a thermal Maxwell-Boltzmann distribution in both sectors, one can perform this calculation analytically and that is how such calculations are typically performed in literature. The problem is that Maxwell-Boltzmann distribution is only valid in the limit particles are non-relativistic. In reality the particles either have a Fermi-Dirac or Bose-Einstein distribution, depending on whether the particles are fermions or bosons. We had decided to perform the energy transfer calculation by taking into account this quantum statistical thermal distribution, for which performing the 8 dimensionl integral is non-trivial.
Until now all the calculation problems I had tackled were a part of a homework or an exam, and hence I knew they had a solution. This was the first problem I encountered that I did not know was even solvable. Obviously, we had a backup plan to evaluate this energy transfer term numerically if a close form analytical solution was not found. And I did develop the code for the numerical evaluation. However, numerically evaluating the energy transfer term at each time step while solving a coupled differential equation of densities, would have dramatically increased the computation time.
So now apart from my own curiosity, I had another reason to support spending time in trying to find an analytical result. And luckily I did find an analytical closed form result! More precisely, I found analytical result at a high, mid and low temperature regimes:
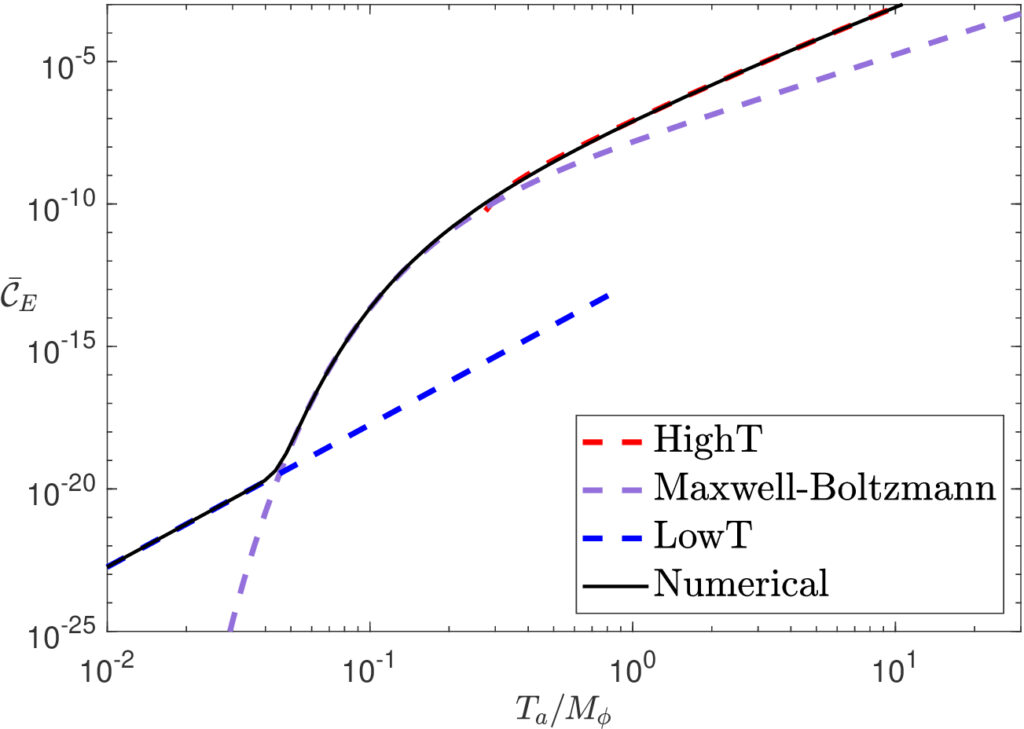
Notice how at high temperatures, the energy transfer rate with Bose-Einstein distribution deviates from that calculated using Maxwell-Boltzmann distribution. In particular the high temperature energy transfer term looks like a beast:
(1) ![\begin{align*} {\mathcal{C}}_{\textrm{high-T}}\propto&\bigg[\frac{4}{3}(1-x)x\log^3\Big(0.2\frac{T_a}{M_{\phi}}\Big)+Y_1(x)\log^2\Big(\frac{T_a}{M_{\phi}}\Big)+Y_2(x)\log\Big(\frac{T_a}{M_{\phi}}\Big)\\&+Y_3(x)\bigg],\end{align*}](/wp-content/ql-cache/quicklatex.com-cb053c6384d0e74aea5b66ff6040664e_l3.png "Rendered by QuickLaTeX.com")
where 
and 
s are some complicated functions I won’t show here. In contrast, the energy transfer term assuming Maxwell-Boltzmann distribution at high temperatures is simply given by
(2) ![\begin{align*} {\mathcal{C}}_{\textrm{MB}}\propto&\bigg[T_a^3-T_b^3\bigg].\end{align*}](/wp-content/ql-cache/quicklatex.com-313b38b7541a8e4a7ec1333b17618ee0_l3.png "Rendered by QuickLaTeX.com")
So one can see that taking into account Bose-Einstein statistics provides a non-trivial logarithmic correction at high temperatures.
Since just performing calculations with Maxwell-Boltzmann statistics is the norm, I was really excited to find this deviation at high temperatures. I imagined this logarithmic dependence on temperature would manifest in interesting ways in our final result where we show density ratio as a function of inflaton decay rates.
Alas, unfortunately it turned out that the final density ratio between the two sectors was primarily determined by the energy transfer rate around the temperatures where the energy transfer rate is well approximated by Maxwell-Boltzmann statistics. In other words, had I just performed the whole analysis using Maxwell-Boltzmann distribution and not wasted months finding analytical result for Bose-Einstein (or Fermi-Dirac) distribution, the final answer would have only deviated by 20% to 50%. In cosmology, where we generally deal with orders of magnitude, no one bats an eye to 50% correction (a hyperbole of course, but you get the spirit).
Nonetheless, even if this calculation of energy transfer rate with quantum statistics does not prove to be of use to others, it is of importance to me because that was the first time I had solved a problem whose solution did not exist before.